Fractions Section 5: Fractions and Decimals
Goal
To help students to use pictures and their reasoning about the meaning of
fractions to
(1) convert decimals to fractions and (2) convert fractions to decimals using
both a part-whole
and a quotient interpretation of fractions.
Big Ideas
The ideas we learned about simplifying fractions from the last section can be
used to
reason about the process of converting fractions to decimals and vice versa.
Converting Decimals to Fractions
To begin this process, we need to first be able to interpret what decimals mean.
For the
decimal .65, we can think of it one of two ways: as six-tenths and
five-hundredths, or as
sixty-five hundredths. If we use the second way of thinking about it, then we
have in fact
converted it to a fraction, albeit a fraction that could still be simplified
further. If we think
of .65 as 6/10 and 5/100, then we can use pictures to help us think about what
this
might be in terms of a single fraction. The picture below represents 6/10 and
5/100:
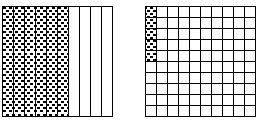
We can turn the block with the tenths into hundredths by
drawing 9 equally spaced
horizontal lines. Then we can combine the shaded regions into one block,
yielding
65/100:

We can further simplify this fraction by grouping the
hundredths into groups of five-hundredths.
Doing this yields the following picture:
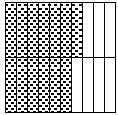
In this picture, we can see that each part that contains five-hundredths is 1/20
of the
whole, because it takes 20 of them to make a whole. Since .65 makes 13 of those
pieces, we know that .65 is equivalent to thirteen 1/20's, or 13/20. Note that
there is no
other way of grouping the hundredths into larger size pieces such that the
larger pieces
both evenly partition the shaded region and the whole. Thus, this is the
fraction in
simplest form.
Converting Fractions to Decimals
Suppose that we wanted to convert 3/4 into its decimal representation. The goal
then
would be to find some fraction that is equivalent to 3/4 and whose denominator
is some
power of ten.
Strategy 1: One way to do this is to start with tenths, and continue with
increasingly
smaller sized pieces (1/100's, 1/1000's, etc.) until we finally get a
partitioning that can
be divided evenly into fourths. Tenths will not work, because there is no way to
group 10
tenths into four equal groups evenly. But hundredths will work:
Note that in each of the four parts, there are 25/100.
Then three of the fourths would be
75/100, or .75.
Strategy 2: A second method that builds on a part-whole understanding of
fractions is
really partitioning with added constraint that we have to respect the division
into tenths,
hundredths, etc. We start by divvying out tenths into four groups to make
fourths. Of
course, if we do this, we will have two tenths leftover. But we know that each
fourth will
be more than 2/10 and less than 3/10.
We can take the remaining two-tenths and divide them into
ten pieces each, so that
each of the smaller pieces would be hundredths. Doing this yields 20/100, which
can be
evenly distributed among the four groups.
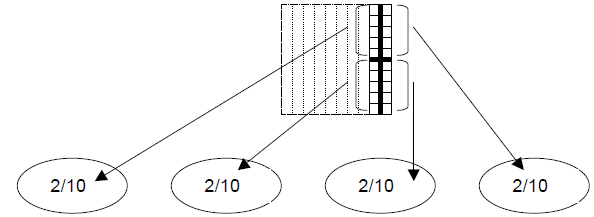
When the 20/100 are evenly distributed among the 4 groups,
each group will get 5/100.
This will give each group a total of 2/10 and 5/100, or .25. Then 3/4, which is
three of
the groups, would be 6/10 and 15/100, which is equivalent to 7/10 and 5/100, or
.75.
Strategy 3: A third method starts with 3/4 being interpreted as a quotient from
3 ÷ 4.
Using a sharing interpretation of division, we ask the question, If 3 were split
among 4
groups evenly, how much would each group get? To answer this question in terms
of a
decimal representation, we use the same technique as above, but instead of
starting
with 1, we start with 3. Then we partition each of the 3 ones into tenths, and
try to
distribute them evenly among the four parts. If we do this, each group will get
7/10, with
2/10 leftover. Then we would divide each of the 1/10s into ten parts to get
hundredths,
and distribute the resulting 20/100 evenly among the four groups so that each
group
had 7/10 and 5/100, or .75. This would be the amount that each of the four
groups
would get if 3 were evenly split among them.
(We can also use a measurement interpretation by asking how many 4s are in 3. We
could divide the 4 into 100 equal pieces so that each resultant piece was 1/100
of 4.
This would give us 25 pieces in each of the 4 ones. Then we would partition the
3 ones
in three into 25 pieces so that we could make a comparison between the 3 and the
4.
We would find that 3 contains 75 pieces of the 100 pieces in 4. So 3 is 75/100,
or .75, of
4.)







